Articles - THE PROBLEM OF INFINITE SLOPE ANALYSIS

Infinite slope analysis is a model generally accepted as a means of evaluating the potential for a slope to generate a mudflow. It is a form of limit equilibrium analysis used to calculate a safety factor against shear sliding of a slab-like surficial mass having a constant thickness on a slope of constant gradient and assuming a saturated zone of constant depth at the base of the mass. The underlying assumption is that the movement of such a relatively rigid mass as an initial shear failure is a necessary precursor to the loss of shear strength of that mass so that flowage can occur. The safety factor for such a geometry is calculated the same way as for deep-seated failures, i.e., using the Mohr-Coulomb model for the total shear strength that can be mobilized along the base of the surficial mass, divided by the stress due to the component of the gravitational force acting along that surface. Without going into the derivation, the total shear strength that can be mobilized at the base of the surficial mass is expressed as:

c + (γz cos 2β - u) tan φ (1)

which is a modification of the Mohr-Coulomb model known as the Terzaghi effective stress model. In this model, c is the effective cohesive strength, γ is the unit weight of the mass, z is the vertical thickness of the mass, β is the angle the slope makes with horizontal, u is the pore water pressure at the base of the section, and φ is the angle of internal friction. It is to be noted that the dimensions of the units are force per unit area.

The stress due to the gravitational force acting down the postulated surface of shear at the base of the surficial zone is calculated as:

γz sinβ cosβ. (2)

Dividing expression (1) by expression (2) gives the safety factor, and this is the method used invariably in geotechnical engineering reports submitted to the City of Malibu (see Sec. 6.2.3.3, Malibu City "Guidelines for the Preparation of Engineering Geologic and Geotechnical Engineering Reports," Feb., 2002) as well as probably all other jurisdictions in southern California, and possibly throughout the State, to satisfy concerns regarding the potential for mudflow.,

The movement of a slab-like surficial mass as a unit in practice is seldom observed to occur over great distance. What appears to happen is that in the initiation of such movement, intergranular contacts are momentarily disrupted in the saturated section and, before they can be regained to again give the mass shear strength, flow occurs. At least that is one theory. But all this is prologue to the real problem of infinite slope analysis as used in geotechnical practice. That problem arises from the manner in which the geotechnical engineer obtains the strength data, and in particular the cohesion, c, of equation (1). It is common practice to use what is referred to as intercept cohesion for the value of c. An example of the data used for this is shown in Figure 1. Such data can be obtained in several of ways, but the most common is through the use of the direct shear apparatus. However, that machine is unsuitable for determining data from trials with normal stresses lower that about 1,000 pounds per square foot. Consequently, the linearity attributed to the data, as indicated by the straight lines projected to the ordinate is simply guesswork.

Cohesive strength in surficial materials such as soil is almost entirely due to the attraction of clay particles to each other because of their bi-polarity. This strength dissipates with increasing moisture content, and in the saturated condition it is lost entirely. Therefore, the results of the direct shear data apply, at most, only to the moisture condition of the sample which is generally low and certainly not saturated. In other words, the safety factor calculated using infinite slope analysis, even if valid, applies only to a slope in which the surficial materials have the same moisture content as that present during the direct shear runs. Of course, then, when the surficial materials in a slope receive ground water from rain, or irrigation, the cohesive strength, and consequently the safety factor, becomes significantly reduced.

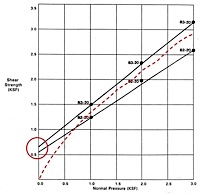
Figure 1. Typical Plot of Direct Shear Tests Data.

The linear character of the envelopes are assumed. The use of the term "pressure" is incorrect except in the case of a saturated undrained sample. The normal load produces a normal stress. The shear strength value is that of the shear stress at failure. A curved envelope, added as the red dashed line, is equally valid in the interpretation of these data. Interceptions of the linear envelopes with the ordinate, encircled, are simply assumed. The data can be interpreted either to show substantial magnitudes of cohesion or zero cohesion.

At lower normal loads near the surface, that actually are present in the field, cohesion is generally thought to be considerably less than that of intercept cohesion values. For example, Taylor and Cripps (1987, pp. 424-439, Figs. 13.9, 13.11, 3.13 ) in their discussion of the strength of weathered materials show that "fully weathered" rocks have zero cohesion.

CAMPBELL'S SOIL-SLIP STUDY

A study by Campbell (1975), which is excellent as well as relevant to Malibu's geology, treats the mudflow risk in terms of its initiation as a slab failure. Consistent with other investigators, he notes (op. cit., fn, p. 19) that in infinite slope analysis the intercept cohesion is assumed to be zero "... for shallow granular materials." However, his main thesis concerning the manner in which a "slab slide" or "soil slip" (op. cit., p. 3) becomes a flow is mainly of interest for present purposes. Concerning this he states (op. cit., p. 25):

Once a slab of soil becomes detached at an underlying slip surface and at the margins and begins moving, part or all of the mass is effectively remolded by its own motion, and it changes from a rigid slab to a viscous fluid. As it moves downslope, the material flows together into a relatively narrow stream moving down established drainages - ravines, gullies, swales, and so on - as a discrete slug.

However, to equate the risk of mudflow only to this remolding mechanism I believe to be a serious mistake. Evidence for this is nowhere better illustrated than in Campbell's description of the Newton Canyon mudflow failure of December 29, 1965 (op. cit., pp. 42 - 46) in which the landslide scar extended from just below Castro Peak at elevation 2824 about 2,000 lineal feet down a narrow channel to its mouth at a point about 1,000 east of Latigo Canyon Road. That channel has an average gradient of about 0.45, i.e., 24.2 degrees from horizontal. From its mouth, the debris spewed outward and swept away everything in its path including a house and its occupant, and an automobile.

Some weeks afterward, Dr. Paul Merifield, Dr. Donald Lamar, and I, traversed the entire length of the channel. We found it to be swept entirely clean of the colluvial and alluvial materials that during many years previously had collected in it. At the channel mouth the sides 10 feet or more above the bottom had been scoured free of all loose material and chaparral. This clearly indicated that debris had passed by there as a wave crest much higher than the height of the channel materials before the failure. To postulate the initiation of this mudflow as a single slab failure is of course untenable, and even a series of them developing successively upstream seems unlikely because where observed, they appear to stabilize after a few feet of movement. A more reasonable mechanism is one involving an initial seepage condition in the debris at the mouth of the channel similar to that which initiates piping.

The Newton Canyon mudflow was the result of a 50-year storm. In the previous 24 hours on the day of the failure, the Malibu Lakeside rain age (LACFCD Station 4B,) 2.3 miles northeast of Castro Peak, had recorded, probably at 1600 hours, 10.28 inches in the previous 24 hours, after a period of 35 days during which almost no rain had fallen. Station 4B is at about elevation 750. Therefore, considering the known local orographic effect, the rain depth immediately around Castro Peak probably was in excess of 13 inches (Bruington, 1971, Fig. C-1.14). Considering the catchment area of the channel, about 50 acres, the channel materials must have become nearly saturated. Indeed, rough calculations suggest that the storm would have produced a rain volume as much as 180 times the porous volume of the channel materials!

An alternative explanation of mudflow development in such circumstances is based on a series of successive failures induced by spring flow. One can postulate that initially, seepage from the materials at the channel mouth would have eroded a small, steep-sided spring face. The consequent increase in spring flow together with the seepage force would have caused that face to fail and in doing so produce a similar larger spring face. Repetition of this process would quickly extend to involve the debris across the entire width of the channel. Once the flow started, a lower reach of the channel would have been cleared of debris giving momentum to subsequently failed sections great enough to pile over any debris lower in the channel which had come to rest or was moving more slowly. It is this kind of process, in a sense feeding on itself, that would have "remolded" the material so that its shear strength was lost. In this failure scenario, there is no mechanism requiring a change from slab movement to fluid flow. .

CONCLUSION

The mudflow is by far the most dangerous type of landslide that commonly affects residential property, because it occurs rapidly and without obvious warning of pending failure. The use of infinite slope analysis provides a safety factor against a shallow surficial shear landslide, more or less as a slab which may or may not remold itself into a flow, but it provides no information whatsoever regarding the risk of a mudflow from that same slope originating as the progressive upslope spring-induced failure mechanism. Even in the case of the shear slide, infinite slope analysis is questionable because, as commonly utilized by geotechnical engineers, a relatively large value of cohesion is necessary to produce a safety factor of 1.5. Typical values for the frictional strengths of soils are not high enough to produce safety factors acceptable for planning purposes. When employed with low values of cohesion, i.e, values much less than those obtained by postulating linear intercept cohesions, as commonly is assumed by geotechnical engineers, the results are less than unity and therefore meaningless.

The continued acceptance by the City of Malibu and other public agencies of a safety factor against mudflow based on infinite slope analysis is difficult to understand. It is well recognized that the use of intercept cohesion based on direct shear data is improper. Eventually, the surficial failure of a slope approved by the City based on acceptance of infinite slope analysis will lead to legal action and possibly the need for doctors or morticians. To avoid this, it would be wise for the City to officially recognize the limitations of infinite slope analysis. In fact, it would be prudent to abandon infinite slope analysis as a design criterion and require instead recommendations from geotechnical consultants for one or more devices to prevent mudflows from developing. Failing this, and considering the wide use of infinite slope analysis by local municipalities, the entire matter seems worthy of investigation by some organization such as the California Joint Powers Insurance Authority.

* * *